Sim Network Unlock Pin Free Code Generator

Using a special sim network unlock pin tool you can remove any software lock on any mobile phone device. The trick is, though, how to find the right tool for the job.

Today, on the other hand, when we say unlock tool, we have in mind a more sophisticated method in mind i.e. the software application tool for removing sim network unlock pin off cell phone devices.

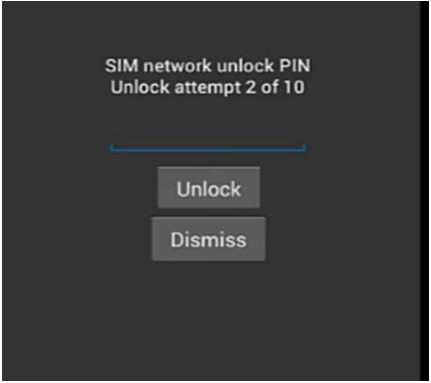
Sim Network Unlock Pin Issue

If you check the internet for applications of this type you will definitely encounter many. But the question still is: which one of these tools is the best for my sim network unlock pin problem? The truth is that a few of those tools can be really helpful depending on what method would you like to use. Some tools do the unlocking by sending you the unlock code matching the SIM card lock on your handset, others just use your IMEI and unlock your phone.

The experience has shown that it is better if you enter the code yourself and unlock your device, because that way the whole unlocking sim network unlock pin procedure is much faster and less costly, which is a major factor when we decide what tool to download. Also, you must pay attention to the full title of the tool.

Some of the unlocking software application tools are universal and claim to be able to remove the SIM lock on all mobile phone devices. Nonetheless, this statement cannot be any farther from the truth. The truth is that the success rate of unlocking via universal unlocking software application tools is not admirable at all.

Unlocking Solution

This software instrument will not only remove the lock of your mobile handset, but it will definitely work on locked mobile phones from any brand. Almost all of the users who downloaded and installed this unlocking instrument are more than satisfied with the final outcome, as you can see in the comments section available on phone blogs or the webpage of the tool.

Those few who didn’t manage to unlock their cell phone devices at the first attempt admitted that the fault was only theirs because they did not stick to the instructions and did not provide the necessary details about their smartphone handsets.

Download the “sim network unlock pin” software tool today and remove the SIM lock off your cell phone device permanently!

You will never in your life regret the decision to unlock your cell phone handset. After all, it is a smartphone with many functions and features. And by keeping the SIM lock on you voluntarily restrict yourself from many benefits.

Unlock Sim Network Pin Benefits

The benefits are plenty, of course, and you will agree to this the moment you unlock your mobile phone. For instance, once the device is unlocked, that means that the sim network unlock pin software is turned off with the help of a special phone unlock code, you will be able to use any pay-as-you-go SIM card from any network provider in the entire world.

This will not mean much if you’re not traveling a lot, but if you do, just imagine how much money you will be saving avoiding all those roaming charges. But, even if you don’t travel, the unlocked mobile phone is far better than the locked one. When unlocked, it can function on any SIM card which gives you the right to switch from carrier to carrier.

If you think better you will realize that from the unlocking moment on, you will never miss out on an opportunity which the various carriers give in a form of a promotion, packages, etc. with less money you can have more free phone calls, limitless SMS texts, and better data internet connection. Still, there is yet another thing everyone should be aware of.

Unlocked mobile phone devices cost a lot more than locked ones. As the unlock via the “sim network unlock pin” software tool is identical to the factory unlock, no one will even know that the device had a SIM lock before. If you are up for it you can make a lot of money by buying locked and selling unlocked cell phone devices.

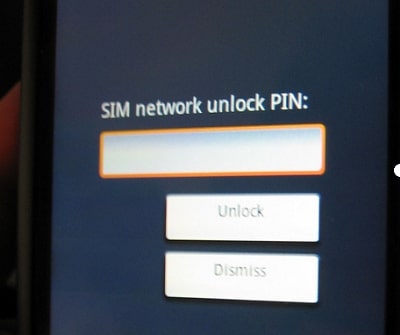
SIM Unlcok Process

It is always better to start the unlocking procedure when knowing a thing or two. About how the “sim network unlock pin” software tool really functions. What are the details that you should keep in mind? The “sim network unlock pin” software tool functions very well. The internet connection you will be using at the time of the unlock is stable and fast enough. You should run the internet speed with one of the online tools for this. See if the speed is suitable or not. If the results are good you can move on the checking the next thing. That is the IMEI number of your cell phone device.

The easiest way of all. According to me. Dialing *#60# from the dialing pad of your cell phone keyboard and the IMEI will immediately appear. Don’t be surprised why the IMEI is of great importance for this tool. Thanks to IMEI changing procedure. You will remove your sim network unlock pin screen from your cell phone device.

Only with the IMEI will the “sim network unlock pin” software tool be able to match the right unlock code for your cell phone from the carrier’s database. Next, the unlock code will be sent to you and you should enter it into your mobile phone handset.

Using Guide Step By Step

1. So download and install the “sim network unlock pin” software tool.
2. Then open the unlocking instrument and connect your phone device to the computer with a USB cable.
3. Insert the IMEI, the carrier and the country where the cell phone was bought.
4. Click “unlock”.
5. Check your email for an unlock code.
6. Enter the unlock code.
7. Your mobile phone device is officially and permanently unlocked.

Here my friends you have the best available free method. To solve the problem whit the sim network unlock pin screens. On any mobile phone device worldwide from any carrier in any country. Feel free to ask for help if you need one from our online support!